Collision detection in AniSprite

Collision detection is not a very complex subject, but it is a broad subject. There are different algorithms that address different special cases of collision detection. It is impossible to come up with a single, "universal best" algorithm that suits all needs; it is even very hard to strike an acceptable compromise (also because collision detection is one of the essential, "key", algorithms in any animation engine, and it is not to be compromised). Microsoft, considering this, decided not to put collision detection in DirectDraw at all ("better not at all than not working well", hmmm, this does not sound like Microsoft).

AniSprite is a 2-dimensional, bitmap based, sprite animation engine. As such, AniSprite is much more specialized than DirectDraw and, therefore, choosing a collision detection algorithm makes a lot more sense. (You can still use a home-grown algorithm if the one of AniSprite is inappropriate for your requirements.)

Like all collision detection algorithms, the one used by AniSprite is optimized for speed. Below is a list of properties (or implementation details) on the collision detection algorithm of AniSprite:

All sprites have a bounding box. This is trivial in the case of a bitmap based animation engine: the size of the bounding box is the size of the image. AniSprite uses the bounding box to quickly reject collisions: when the bounding boxes of two sprites do not intersect, the sprites cannot possibly collide.
AniSprite's collision detection is precise at a pixel. A collision, by the way, is defined as an overlap of two sprites. When two sprites "touch" but do not overlap, there is no collision.
Every sprite has an "opaque" level, which lets you specify at what level of opacity (or transparency) an overlap is flagged as a collision. This is useful in the case of alpha-blending and shadows (luma-blending).
You can check every pair of sprites for a collision, or you can use a semi-automatic way to react on collisions via callbacks. By giving only the sprites that can cause collision a "callback", only those are checked. This is quite straight-forward to use and it achieves a significant optimization over the trivial "check all sprites for collisions against all other sprites" scheme.
Furthermore, by default AniSprite only checks for collisions between sprites in the same "layer" (a layer is a category of z-levels, see the AniSprite manual for details). The reasoning behind this idea is that layers often represent a distance from the viewer. A sprite that near to the viewer may obscure another sprite that is far from the viewer (this is technically a collision), but, logically one sprite does not "hit" the other.
A final optimization of AniSprite is the reduction of overhead once a collision has been detected. The collision must be reported, of course, but there is typically no need to report the collision between the same pair of sprites at every clock tick. What AniSprite does (by default) is to report only the changes in the state of collision between two sprites: the sprite gets an event when it enters collision with some other sprite and when it leaves collision with that sprite.

In this paper, I will focus on the semi-automatic collision detection scheme of AniSprite, using a simple "bouncing balls" animation as a vehicle. Given this constraint and given the default operation of AniSprite, what, then, is a collision?

A collision is:

An overlap between two sprites in the same layer.
An event, which AniSprite "fires" by invoking a callback function.
A state: AniSprite keeps per sprite a record of any other sprite that it is "in collision" with.
A relation between a pair of sprites: if a sprite collides with two other sprites, it receives two events (or callback invocations) and two collision states are maintained for that sprite.

Keep a ball on the table

The program that I will implement starts simple: one ball that moves in a straight line over a billiard table and that bounces on the edges of the table. The way that the program does this is by storing the velocity and direction of the ball in the "user data" of the ball sprite and flip the direction when it receives a collision event (a collision with one of the edges of the table). I will skip the code needed to load/create the board and the sprites and focus directly on setting up the collision detection.

Setting up a collision callback

  typedef struct {
    POINT cur;
    POINT next;
  } DELTA, FAR * LPDELTA;

  LPDELTA delta;
  FARPROC lpfn;

  delta = malloc(sizeof(DELTA));
  delta->next.x = rand() % 10;
  delta->next.y = rand() % 10;
  as_SetData(Sprite, AS_DATA_USERDATA, 0, delta);

  lpfn = MakeProcInstance((FARPROC)CollisionCallback, hInstance);
  as_SetData(Sprite, AS_DATA_CALLBACK, AS_EVENT_COLLIDE, (LPVOID)lpfn);

By the way, making a "ProcInstance" of for the callback function is only needed for 16-bit code. In Win32, this call does nothing (but it does not harm either).

AniSprite supports one special collision: a sprite can collide against any rectangle that is set for the board. There is no collision when the sprite is completely inside this rectangle, the sprite collides with this rectangle when it is partially outside the rectangle. This rectangle has to be set up explicitly and it may be smaller than the board or larger than it. In our case, making the board's collision box just as big as the board itself is fine.

Another "by-the-way" is the definition of the DELTA structure. The cur field forms the vector for the current displacement (direction and velocity). The field "next" will form the new displacement vector that is used for the next update; it is copied to cur just before moving the sprite at each update. I will need to be able to set the new vector while saving the old vector when handling collisions between sprites.

Setting a collision rectangle for the board

  RECT rect;

  SetRect(&rect, 0, 0,
          as_GetBoardValue(Board, AS_VALUE_WIDTH, 0),
          as_GetBoardValue(Board, AS_VALUE_HEIGHT, 0));
  as_SetBoardData(Board, AS_DATA_COLLIDERECT, 0, &rect);

At every timer tick, the ball sprite should move with "(delta->cur.x, delta->cur.y)" pixels. Now, there is still the callback function to make that must invert either delta->cur.x or delta->cur.y. Actually, the callback must update delta->new instead of delta->cur; this is discussed later in this paper. Checking which edge is hit is trivial, one only needs to consider that the ball might hit two edges at the same time and that, at the time that the collision is detected, the ball may have exceeded an edge.

The collision callback function

DWORD FAR PASCAL CollisionCallback(ASPRITE Sprite, int Event,
                                        DWORD Value, LPVOID Data)
{
  /* ignore "collision off" message */
  if (Value == AS_COLLISION_END)
    return 0L;

  if (Data == NULL)
    return CollideWithBoard(Sprite);
  else
    return CollideWithSprite(Sprite, Data);
}

The collision callback function simply calls a sub-function for either collisions with the board or with another sprite (after filtering out the "collision off" events). This is simply a trick so that I can postpone dealing with sprite-to-sprite collisions until later in this paper. The function that handles sprite-to-board collisions is below:

Board collisions

DWORD CollideWithBoard(ASPRITE Sprite)
{
  RECT FAR *lprc;
  int x, y, width, height;
  LPDELTA delta;
  ASBOARD Board;

  /* get current position and size */
  x = as_GetValue(Sprite, AS_VALUE_XPOS);
  y = as_GetValue(Sprite, AS_VALUE_YPOS);
  width = as_GetValue(Sprite, AS_VALUE_WIDTH);
  height = as_GetValue(Sprite, AS_VALUE_HEIGHT);

  /* get current direction/velocity */
  delta = as_GetData(Sprite, AS_DATA_USERDATA, 0);

  /* a sprite collides with the board's box, find out which edge */
  Board = as_GetData(Sprite, AS_DATA_BOARD, 0);
  lprc = as_GetBoardData(Board, AS_DATA_COLLIDERECT, 0);
  if (x < lprc->left) {
    x = lprc->left;
    delta->next.x = - delta->cur.x;
  } else if (x + width > lprc->right) {
    x = lprc->right - width;
    delta->next.x = - delta->cur.x;
  } /* if */
  if (y < lprc->top) {
    y = lprc->top;
    delta->next.y = - delta->cur.y;
  } else if (y + height > lprc->bottom) {
    y = lprc->bottom - height;
    delta->next.y = - delta->cur.y;
  } /* if */

  /* adjust position */
  as_SetPos(Sprite, x, y);

  /* tell the collision detector that we want another event on the next
   * occasion if we're anew colliding (we moved the sprite out of
   * collision in the code above)
   */
  return 1L;
}

Valuing aesthetics over accuracy, I have introduced an error in the above routine by resetting the sprite to a board's edge if it has collided with it. In fact, I should have let it bounce back from the edge, like in the figure below.

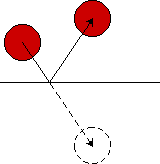
The position of the sprite on the board at each timer tick is a snapshot and a collision may well occur precisely in the mid between two snapshots. This makes it appear as if the ball bounces without being ever near the board's edge, however, and therefore I chose to put the ball against the edge. Highly inaccurate from a kinetic point of view, but animation is playing tricks with human vision anyway (so one more trick does no harm).

There is one subtle problem with the above code. After we handled the collision the sprite's position was adjusted to move back into the bounds of the board. That is, the collision has been resolved, it has vanished. AniSprite is unaware of this, however. It has detected the collision, inserted it in the sprite's "collision state" list and invoked the callback... but it does not recheck the collision after returning from the callback. Now consider the sequence of events from the animation below:

The first collision was reported and the callback moved the sprite back into the board. At the third timer tick, there is a second collision with another edge. AniSprite, however, considers this a continuation of the collision reported earlier: the sprite was in collision with the board's collision rectangle at timer tick 2, and it is in collision with the board's collision rectangle at timer tick 3. There is no change in the collision status for the sprite, so no collision is reported at timer tick 3. And the sprite moves off the board.

The fix is, of course, to keep AniSprite informed and the simplest solution is to ask AniSprite to disregard the collision state after return from the callback. To do this, simply return "1" from the callback function. AniSprite will then not save the collision between the sprite and the board's collision rectangle at timer tick 2 and, hence, report a collision at timer tick 3.

Bouncing balls

Now I want to focus on collisions between two (or more) balls. The groundwork is already laid; I just need to implement the CollideWithSprite() function. There is a bit of kinetic theory involved, plus the "gotcha" that two sprites that collide mutually influence each other. That is, if a ball hits an edge of the billiard table, the ball changes direction but the edge of the billiard table does not move. If, on the other hand, a ball hits another ball, both balls change direction/velocity.

Let me start with the physics. The collision is assumed fully elastic, so there is conservation of kinetic energy. Together with the law of conservation of momentum, one can describe the change of direction and velocity of objects after collision. The balls are furthermore assumed to have the same weight, which simplifies the calculations quite a bit.

With these restrictions, a collision in a one-dimensional case will simply swap the velocities of the two balls, as in the figure below.

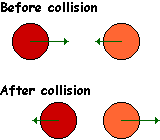
I am skipping the derivation of this reduced one-dimensional case. You will probably already know this or be able to look it up in a physics textbook; if you don't know kinetics, you will need a better teacher than me.

The one-dimensional case is overly simplistic: we are interested in collisions in two dimensions, which add the following complexities (which, actually, are related):

the balls may not move in exactly opposing directions when they hit, they may hit at an angle
the direction of the impulse goes through the centres of the balls (at the time of the collision); this vector may not be aligned to the direction of either of the balls

The kinetic laws tell us that a body only changes velocity or direction if a force is being applied to it. Force has a direction. In our case, the force applied to one ball is caused by it being hit by another ball. The direction of the force is the normal of the surfaces that touch (in absence of friction) and goes through the centres of the two balls that collide. By projecting the motion vectors of both sprites to the imaginary axis through the centres of the balls, the problem reduces to the one-dimensional case described earlier.

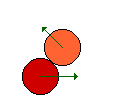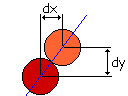
The approach to solve the collision is:

Calculate the angle of the imaginary axis through the centres of the balls with the horizontal axis.
That is: tan a = dy/dx.
Rotate the motion vectors of both balls by the inverse angle (-a); this has the effect of aligning the collision to the horizontal axis.
Swap the horizontal components of the vectors, as in the one-dimensional case; the vertical components of the vectors remain unchanged.
Rotate the vectors back (+a).

Rotating a vector is covered in any book on matrix/vector mathematics or on 3-dimensional graphics. For simplicity, I have used the two equations below; most books pack the equations in a matrix.

x' = x × cosa - y × sina
y' = x × sina + y × cosa

Back to the code: below is the CollideWithSprite() function that reacts on collisions between two sprites. One key issue to point out is that, if two sprites collide, both receive the collision event. In the analysis above, I talked casually about swapping the parts of the vector that align with the axis through the balls' centres. In fact, each callback should only change the vector for the sprite that the event is issued for. If you change both sprites in the first callback, the second callback, for the other sprite involved in the collision, will change both sprites back.

So each callback changes only one sprite. Now, the second callback will need to adjust the second sprite that is involved in a collision based on the original displacement vector of the first sprite. Hence, the "current" displacement vector must be saved per sprite until all collision events are handled.

Sprite collisions

DWORD CollideWithSprite(ASPRITE Sprite, ASPRITE HitSprite)
{
  int x1, y1, x2, y2;
  LPDELTA delta1, delta2;
  double angle;

  /* a sprite collides another sprite, get current position of
   * both sprites
   */
  x1 = as_GetValue(Sprite, AS_VALUE_XPOS);
  y1 = as_GetValue(Sprite, AS_VALUE_YPOS);
  x2 = as_GetValue(HitSprite, AS_VALUE_XPOS);
  y2 = as_GetValue(HitSprite, AS_VALUE_YPOS);

  /* calculate the angle */
  angle = atan2(y2-y1, x2-x1);

  /* get current direction/velocity of both sprites */
  delta1 = as_GetData(Sprite, AS_DATA_USERDATA, 0);
  x1 = delta1->cur.x;
  y1 = delta1->cur.y;
  delta2 = as_GetData(HitSprite, AS_DATA_USERDATA, 0);
  x2 = delta2->cur.x;
  y2 = delta2->cur.y;

  /* rotate vectors to align the collision to the horizontal axis */
  rotatevect(&x1, &y1, -angle);
  rotatevect(&x2, &y2, -angle);

  /* "swap" the horizontal component (but since only the
   * direction/velocity of "Sprite" is modified, there is no
   * need to modify x2)
   */
  x1 = x2;

  /* rotate back (again, rotating the vector of "HitSprite" back
   * is not needed because it is not adjusted)
   */
  rotatevect(&x1, &y1, angle);
  delta1->next.x = x1;
  delta1->next.y = y1;

  return 0L;
}

Details, details, ...

The snippets in this paper illustrate the "richness" of collision detection. None of it is really complicated, but the devil is in the details. There are still a number of limitations and caveats in the code developed so far:

The accuracy of calculations is very limited, due to the use of integers for the displacement vectors. Intermediate results (rotated vectors and such) are also in integers.
When two sprites collide, they overlap by at least one pixel. This should be reset, as was done for collisions between a sprite and the board's rectangle.
As a result of not resetting a collision, and also because of the limited accuracy of the calculations, a collision between two sprites may not cease one timer tick later. If that happens, the sprites stay in collision, but no (more) event is issued for this. The result is that the sprites move happily on top of each other.
Collisions between three or more sprites are not considered (not even in the analysis).

What needs to be done, hence, is to calculate (and store) the displacement in floating point format. This implies that the "current position" of a billiard ball also needs to be maintained in floating point precision, because the current position is adjusted with the delta vector at each iteration. This, consecutively, implies that we need to store the current position of a sprite ourselves, rather than querying AniSprite for the location, because AniSprite only keeps the (integral) pixel positions of a sprite. Resetting the collision of a sprite (the second point of the above list) is rather simple once we calculated the angle. When (x1,y1) and (x2,y2) denote the positions of the two balls in a collision (balls "1" and "2") and "r1" and "r2" are their radii:

x1 = x2 - (r1 + r2) × cosa
y1 = y2 - (r1 + r2) × sina

Actually, we only need to reset one of the two sprites that collide; we might want to check in the event handler (CollideWithSprite()) that the sprite that you handle does still overlap with the other sprite. On the other hand, a double reset should never hurt.

The third issue, which was a result of the first two points, has implicitly been taken care of. This leaves us with the final issue: collisions between multiple sprites. One solution is to consider this a "chained" collision, first one pair, then the other pair. An alternative is to tackle one collision in the current frame and the other in the next frame. In that case, the frame rate better be high; to get a sufficiently high frame rate, I suggest that the "calculation loop" be separated from the "screen update loop". That is, the positions of the sprites are recalculated as frequently as possible, but the screen is refreshed on a fixed frame rate. Uncoupling the "calculation" and "screen update" loops makes that the calculation loop can run much quicker.

For more information and for a complete and working example program that includes the (improved) code snippets in this paper, download the AniSprite evaluation version and look for the file BILLIARD.C.