Candela, Lumen, Lux: the equations
Light is measured with different techniques, and therefore there is a handful of related, but different, units of measurements. This article gives a brief overview of the most widely used measures and presents a few equations for conversion of one measure into another. For convenience, a table with conversion calculators is at the bottom of this page.
Optical radiation covers a broad spectrum, including infrared and ultraviolet light. For the sake of brevity, this article focuses on visible light (the field of photometry).
Candela
 The candela (unit cd) has its origin in the brightness of a
"standard candle", but it has received a more precise definition in the International
System of Units (SI) —and at that time the unit was also renamed from “candle”
to “candela”.
The candela (unit cd) has its origin in the brightness of a
"standard candle", but it has received a more precise definition in the International
System of Units (SI) —and at that time the unit was also renamed from “candle”
to “candela”.
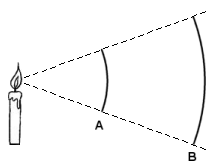
The candela measures the amount of light emitted in the range of a (three-dimensional) angular span. Since the luminous intensity is described in terms of an angle, the distance at which you measure this intensity is irrelevant. For ease of illustration, in the picture at the right the three dimensions have been flattened to two. In this picture, screen B would catch exactly the same amount of light rays (emitted from the light source) as screen A —provided that screen A were removed to not obscure screen B. This is because screen B covers the same angle as screen A.
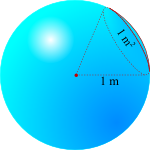 The angular span for candela is expressed in steradian, a measure without unit
(like radian for angles in a two-dimensional space). One steradian on a
sphere with a radius of one metre gives a surface of one m2.
A full sphere measures \( 4\pi \) steradians.
The angular span for candela is expressed in steradian, a measure without unit
(like radian for angles in a two-dimensional space). One steradian on a
sphere with a radius of one metre gives a surface of one m2.
A full sphere measures \( 4\pi \) steradians.
See the section on lux for the relation between candela and lux.
Lumen
If you look at LEDs, especially high-brightness LEDs, you may notice that the LEDs with a high luminous intensity (in candela or milli-candela, mcd) typically have a narrow apex angle. Similarly, LEDs with a wide apex angle typically have a relatively low luminous intensity. The same is true for halogen spots with reflector: those with a narrow-beam reflector have a higher rating in candela than the “floodlight” spots of the same power.
The cause for this relation is the total energy produced by the LED. LEDs of a specific class (for example, “high flux”) all produce roughly the same amount of luminous energy. However, when a LED emits its total energy in a beam with a narrow angle, the intensity will be greater (in the direction of that angle) than when the same energy had been emitted over a wide angle.
The lumen (unit lm) gives the total luminous flux of a light source by multiplying the intensity (in candela) by the angular span over which the light is emitted. With the symbol \( \Phi_v \) for lumen, \( I_v \) for candela and \( \Omega \) for the angular span in steradian, the relation is:
\[ \Phi_v = I_v \cdot \Omega \]If a light source is isotropic (meaning: uniform in all directions), \( \Phi_v = 4\pi\ I_v \). This is because a sphere measures \( 4\pi \) steradians. See the topic on apex angles to get the three-dimensional angular span \( \Omega \) from an opening angle.
As a frame of reference, a standard 120V/60W light bulb is rated at 850 lm, and the equivalent 230V/60W light bulb is rated at 700 lm. A low voltage (12V) tungsten halogen lamp of 20W gives approximately 310 lm.
Lux
 Lux (unit lx) is a measure of illumination of a surface. Light meters often
measure lux values (or footcandles, but these are directly related: one
footcandle is 10.764 lx). Formally, lux is a derived unit from lumen, which is
a derived unit from candela. Yet, the concept of lux is more easily compared to
candela than to lumen.
Lux (unit lx) is a measure of illumination of a surface. Light meters often
measure lux values (or footcandles, but these are directly related: one
footcandle is 10.764 lx). Formally, lux is a derived unit from lumen, which is
a derived unit from candela. Yet, the concept of lux is more easily compared to
candela than to lumen.
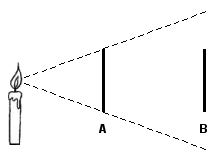
The difference between lux and candela is that lux measures the illumination of a surface, instead of that of an angle. The net result is that the distance of that surface from the light source becomes an important factor: the more distant that the surface is from the light source, the less it will be illuminated by it. In the picture at the right, screen A has the same size as screen B.
One steradian on a sphere with a radius of one metre gives a surface of one m2 (see the section on candela). From this, it follows that at a measuring distance of 1 metre, the values for candela (lumen per steradian) and lux (lumen per m2) are the same. In general, measurements in lux can be converted to and from candelas if the measurement distance is known. Note that when measuring LEDs, the virtual origin of the light source lies a few millimetres behind the physical point source because of the lens of the LED —this becomes relevant when measuring LEDs at a short distance.
Luminance
Luminance is a measure for the amount of light emitted from a surface (in a particular direction). The measure of luminance is most appropriate for flat diffuse surfaces that emit light evenly over the entire surface, such as a (computer) display. Luminance is a derived measure, expressed in Candela per square metre (\( cd / m^2 \)). An alias for the unit \( cd / m^2 \) (unofficial, but still commonly used) is “Nit”.
Luminance and illuminance ("Lux") are related, in the sense that luminance is a measure of light emitted from a surface (either because of reflection or because it's a light-emitting surface), and illuminance is a measure for light hitting a surface. Assuming a perfect diffuse reflecting surface, you can multiply the measure in “Nits” by \( \pi \) to get the equivalent value in Lux. That is, with \( L_v \) for Luminance and \( E_v \) for Lux:
\[ E_v = L_v \cdot \pi \]As with Lux, there are several older units for luminance, of which the foot-lambert is probably the most common (because of its 1-to-1 relation with the footcandle on a Lambertian-reflecting surface). These older units are easily converted to candela per square metre by multiplying them with a scale factor. For foot-lambert, the scale factor is 3.425.
Apex angle
 Since the lumen and the candela measures are related through the viewing angle
(or apex angle), it is useful to know how this angle is defined.
Since the lumen and the candela measures are related through the viewing angle
(or apex angle), it is useful to know how this angle is defined.
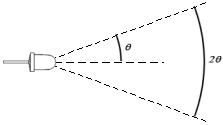
One measures the angle between the axis where the light source gives its highest luminous intensity and the axis where that intensity is reduced to 50%. In the picture at the right, this angle is denoted with \( \theta \). The apex angle is twice that angle (meaning \( 2 \theta \)).
Observe that the reduction of intensity to 50% is based on a linear scale, but that our perception of brightness is not linear. The CIE has standardized the relation between luminous intensity and perceived brightness as a cubic root; other sources claim that a square root better approximates this relation. See also the page on colour metric.
The three-dimensional angular span for an apex angle, using \( \Omega \) for the angular span (in steradian) and \( 2 \theta \) for the apex angle, is:
\[ \Omega = 2\pi \left( {1 - \cos {2 \theta \over 2}} \right) \]Lighting efficiency
There are ample ways to illuminate a surface or a room: incandescent lamps, fluorescent tubes, LEDs, tungsten-halogen bulbs, electroluminescent sheets, and others. These are often compared in their efficiency of turning electrical energy to luminous energy.
The official name for lighting efficiency is “luminous efficacy of a source”. This should not be confused with the “luminous efficacy of radiation”, which disregards losses due to heat generation and others (and therefore gives significantly higher values). The lighting efficiency is measured in lm/W (lumen per Watt).
Lighting efficiency is often expressed as a percentage, based on the theoretical maximum value of lighting efficiency of 683.002 lm/W (at a wavelength of 555 nm). For example, at the time of this writing, a white 1 Watt “lumiled” can reach an efficiency of over 100 lm/W, giving an efficiency of 15%. While this may seem low, LEDs are actually quite efficient in comparison with other lighting methods.
Equations
The equations in this sections are given without further explanation or derivation. For details, please refer to the technical literature, or Wikipedia.
| From | To | Given | Equation |
|---|---|---|---|
| Candela (\( I_v \)) | Lumen (\( \Phi_v \)) | apex angle α | \( \Phi_v = 2\pi I_v\left( {1 - \cos {\alpha \over 2}} \right) \) |
| Lumen (\( \Phi_v \)) | Candela (\( I_v \)) | apex angle α | \( I_v = {\Phi_v \over {2\pi \left( {1 - \cos {½ \alpha}} \right)}} \) |
| Lumen (\( \Phi_v \)) | Lux (\( E_v \)) | surface area A (m2) | \( E_v = {\Phi_v \over A} \) |
| Lux (\( E_v \)) | Lumen (\( \Phi_v \)) | surface area A (m2) | \( \Phi_v = E_v \cdot A \) |
| Candela (\( I_v \)) | Lux (\( E_v \)) | measuring distance D (m) | \( E_v = {I_v \over {D^2}} \) |
| Lux (\( E_v \)) | Candela (\( I_v \)) | measuring distance D (m) | \( I_v = E_v \cdot D^2 \) |
As an example, if the data sheet of a high brightness LED mentions that it produces 1500 mcd (1.5 cd) at an apex angle of 70°, that LED gives:
\[ \eqalign{ \Phi_v &= 2\pi \cdot 1.5\left( {1 - \cos {70^\circ \over 2}} \right) \cr &= 3\pi \left( {1 - \cos 35^ \circ } \right) \cr &\approx 1.70\,{\rm lm} } \]Conversion calculators
Based on the equations developed and presented above, the table below allows you to quickly convert one measure into another.
Evaluation
The outcome of the equations (and the calculators based on them) may differ from the data given by a LED or spotlight manufacturer, or from what you measure with a Lux meter, for several reasons. The manufacturer may specify the luminous intensity (in candela or milli-candela) perpendicular to the light source, instead of the average value over the apex angle. Another complexity is that the values for candela, lumen and lux are standardized for light with a wave length of 555 nm, or green light. For LEDs of a different colour, a weighting function should be applied, using a standardized model of the human eye. Standard Lux meters have, at best, only filters for daylight and incandescent light, and may therefore deviate significantly for LEDs (even white LEDs, as the spectrum is not the same as for incandescent lamps).

